Rozgrzej się dla mózgu: czy możesz rozwiązać problem z fałszywymi monetami? Sprawdź to!

Matematyk ma tylko trzy próby, więc nie możesz zważyć każdej monety osobno. Musisz podzielić je na stosy i położyć je na wadze po kilka sztuk na raz, stopniowo zbliżając się do fałszywej.

Powiedzmy, że matematyk postanawia podzielić 12 monet na trzy stosy po cztery monety. Następnie położył cztery monety na każdej skali. To ważenie może dać dwa wyniki. Rozważmy każdy z nich.

1. Waga dwóch stosów monet była taka sama. W konsekwencji wszystkie pieniądze, które się w nich znajdują, są prawdziwe, a fałszerstwo znajduje się gdzieś wśród czterech nieważonych monet.

Aby śledzić wynik, matematyk zaznacza wszystkie skrypty zerem. Następnie bierze trzy z nich i porównuje je z trzema nieważonymi monetami. Jeśli ich waga jest równa, to pozostała (czwarta) nieważona moneta jest fałszywa. Jeśli waga jest inna, matematyk umieszcza plus na trzech nieoznakowanych monetach, jeśli są one cięższe niż te z zerami, lub minus, jeśli są lżejsze.

Potem bierze dwa monetyoznaczone plusem lub minusem i porównuje ich wagę. Jeśli jest taki sam, pozostała kopia jest fałszywa. Jeśli nie, matematyk patrzy na znaki: wśród monet z plusem podróbka będzie ta, która jest cięższa, wśród monet z minusem, ta, która jest lżejsza.

2. Waga dwóch stosów monet nie była taka sama.

W takim przypadku matematyk musi postępować w następujący sposób: oznaczyć pieniądze na dużym stosie plusem, na lekkim stosie - minusem, na stosie nieważonym - zerem, ponieważ wiadomo, że fałszywa kopia była na wadze.

Teraz musisz przegrupować monety, aby pasowały do ​​dwóch pozostałych ważeń. Jednym ze sposobów jest wzięcie zamiast trzech monet z plusem trzech monet z minusem i umieszczenie na ich miejscu trzech monet z zerem.

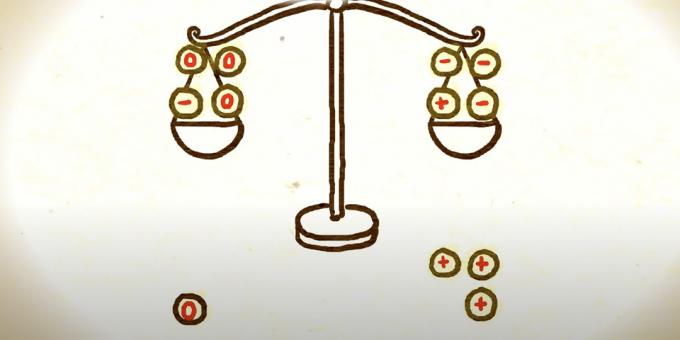
Oto trzy możliwe opcje. Jeśli ta waga, która była cięższa, nadal przeważa, to albo stara moneta ze znakiem plus jest cięższa od reszty, albo moneta ze znakiem minus pozostałym na drugiej skali jest lżejsza. Matematyk musi wybrać dowolną z nich i porównać ze wspólnym wzorem, aby znaleźć podróbkę.

Jeżeli szalka, która była cięższa, stała się lżejsza, to jedna z trzech monet ze znakiem minus przesuniętym przez matematyka jest najlżejsza. Teraz musi porównać dwa z nich na wadze. Jeśli wyniki są remisowe, trzecia moneta zostanie sfałszowana. W przypadku nierówności łatwiejsze jest fałszywe.

Jeśli miski są wyważone po wymianie, jedna z trzech monet wyjętych z wagi ze znakiem plus jest cięższa niż pozostałe. Matematyk musi porównać dwa z nich. Jeśli są równe, trzecia jest fałszywa. W przypadku nierówności podróbka to ta, która jest cięższa.

Cesarz kiwa głową z aprobatą, słuchając rozumowania matematyka, ale nieuczciwy gubernator idzie do więzienia.

Ta łamigłówka jest tłumaczeniem filmu TED-Ed.