Problem królików średniowiecznego matematyka Leonarda Fibonacciego

Zobaczmy, jak rośnie liczba królików w pierwszych sześciu miesiącach:

Miesiąc 1. Jedna para młodych królików.

Miesiąc 2. Nadal istnieje jedna oryginalna para. Króliki nie osiągnęły jeszcze wieku rozrodczego.

Miesiąc 3. Dwie pary: oryginalna po osiągnięciu wieku rozrodczego + para młodych królików, które urodziła.

Miesiąc 4. Trzy pary: jedna oryginalna para + jedna para królików, które urodziła na początku miesiąca + jedna para królików, które urodziły się w trzecim miesiącu, ale nie osiągnęły jeszcze dojrzałości płciowej.

Miesiąc 5. Pięć par: jedna oryginalna para + jedna para urodzona w trzecim miesiącu życia i osiągająca wiek rozrodczy + dwie nowe pary, którym urodziły + jedna para, która urodziła się w czwartym miesiącu, ale jeszcze nie dotarła dojrzałość.

Miesiąc 6. Osiem par: pięć par z ostatniego miesiąca + trzy nowonarodzone pary. Itp.

Aby było jaśniej, zapiszmy otrzymane dane do tabeli:

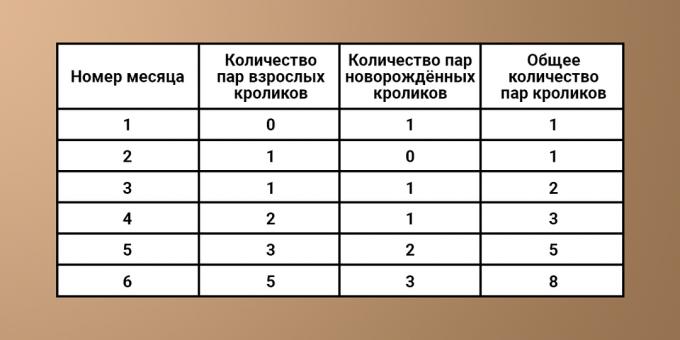
Jeśli dokładnie przejrzysz tabelę, możesz zidentyfikować następujący wzór. Każdorazowo liczba królików obecnych w n-tym miesiącu jest równa liczbie królików w (n-1) -tym miesiącu poprzednim, zsumowana z liczbą nowo narodzonych królików. Z kolei ich liczba jest równa całkowitej liczbie zwierząt w (n - 2) miesiącu (czyli dwa miesiące temu). Stąd możesz wywnioskować

formuła:

fa_n = F._{n - 1}+ F._{n - 2},

gdzie F._n - łączna liczba par królików w n-tym miesiącu, F_{n - 1} To całkowita liczba par królików w poprzednim miesiącu, a F_{n - 2} - łączna liczba par królików sprzed dwóch miesięcy.

Policzmy za jego pomocą liczbę zwierząt w kolejnych miesiącach:

Miesiąc 7. 8 + 5 = 13.

Miesiąc 8. 13 + 8 = 21.

Miesiąc 9. 21 + 13 = 34.

Miesiąc 10. 34 +21 = 55.

Miesiąc 11. 55 + 34 = 89.

Miesiąc 12. 89 + 55 = 144.

Miesiąc 13 (początek przyszłego roku). 144 + 89 = 233.

Na początku 13. miesiąca, czyli pod koniec roku będziemy mieć 233 pary królików. Spośród nich 144 pary będą dorosłe, a 89 będzie młodymi. Wynikowa sekwencja 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233 zwane liczbami Fibonacciego. W nim każda nowa ostateczna liczba jest równa suma poprzednie dwa.